2023年蓝桥杯省赛C/C++大学A组代码

发表于 2025-02-19 更新于 2025-05-10 分类于蓝桥杯阅读次数：本文字数： 3.5k 阅读时长 ≈ 13 分钟

~~好几道题还没做。~~
算了，寒假里做几道放几道呗

[蓝桥杯 2023 省 A] 填空问题

题目描述

A. 幸运数

小蓝认为如果一个数含有偶数个数位，并且前面一半的数位之和等于后面一半的数位之和，则这个数是他的幸运数字。例如是一个幸运数字，因为它有个数位，并且。现在请你帮他计算从至之间共有多少个不同的幸运数字。

B. 有奖问答

小蓝正在参与一个现场问答的节目。活动中一共有道题目，每题只有答对和答错两种情况，每答对一题得分，答错一题分数归零。

小蓝可以在任意时刻结束答题并获得目前分数对应的奖项，之后不能再答任何题目。最高奖项需要分，所以到达分时小蓝会直接停止答题。

已知小蓝最终实际获得了分对应的奖项，请问小蓝所有可能的答题情况有多少种？

提示

第十四届蓝桥杯大赛软件赛省赛 C/C++ 大学 A 组 A-B

解法

填空题，暴！

long long ans1,ans2;//4430091，8335366
// 11~99999999
void solve1(){
    int cnt[40][5]={0};//和为几（1~36），几位数（1~4）
    for(int i=1;i<=9999;i++){
        int w=0,s=0,a=i;
        while(a){
            w++;
            s+=a%10;
            a/=10;
        }
        cnt[s][w]++;
    }
    for(int i=1;i<=36;i++){
        for(int j=1;j<=4;j++){
            int s=0;
            for(int k=1;k<=j;k++){
                s+=cnt[i][k];
            }
            ans1+=cnt[i][j]*s;
        }
    }
}
//答对，答错或者结束比赛
//300题拿了7分，答对1题加10分，答错分数归零。其中分数不可能>=100
void dfs(int t,int s){//题号，分数
    if(s==100)//到达100分时小蓝会直接停止答题
        return;
    if(s==70){
        ans2++;}
    if(t==31)//比赛结束
        return;
    dfs(t+1,s+10);//答对+1
    dfs(t+1,0);//答错分数归0
}
void solve2(){
    dfs(1,0);
}

[蓝桥杯 2023 省 A] 平方差

题目描述

给定，问中有多少个数满足存在整数使得。

输入格式

输入一行包含两个整数，用一个空格分隔。

输出格式

输出一行包含一个整数满足题目给定条件的的数量。

样例 #1

样例输入 #1

1 5

样例输出 #1

提示

【样例说明】

【评测用例规模与约定】

对于的评测用例，；

对于所有评测用例，。

第十四届蓝桥杯大赛软件赛省赛 C/C++ 大学 A 组 C

解法

$ $令奇数和为奇数偶数和为偶数或$ $

#include <bits/stdc++.h>
using namespace std;
signed main()
{
    int l, r;
    cin >> l >> r;
    cout << (r >> 1) + (r & 1) - (l >> 1) + (r >> 2) - (l >> 2) + !(l & 3) << endl;
    return 0;
}

[蓝桥杯 2023 省 A] 更小的数

题目描述

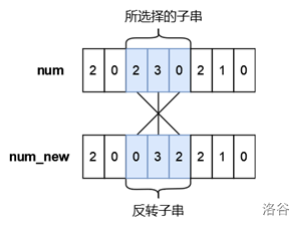
小蓝有一个长度均为且仅由数字字符组成的字符串，下标从到，你可以将其视作是一个具有位的十进制数字，小蓝可以从中选出一段连续的子串并将子串进行反转，最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字满足条件，请你帮他计算下一共有多少种不同的子串选择方案，只要两个子串在中的位置不完全相同我们就视作是不同的方案。

注意，我们允许前导零的存在，即数字的最高位可以是，这是合法的。

输入格式

输入一行包含一个长度为的字符串表示（仅包含数字字符），从左至右下标依次为。

输出格式

输出一行包含一个整数表示答案。

样例 #1

样例输入 #1

样例输出 #1

提示

【样例说明】

一共有种不同的方案：

所选择的子串下标为，反转后的；
所选择的子串下标为，反转后的；
所选择的子串下标为，反转后的；
所选择的子串下标为，反转后的；
所选择的子串下标为，反转后的；
所选择的子串下标为，反转后的；
所选择的子串下标为，反转后的；
所选择的子串下标为，反转后的。

【评测用例规模与约定】

对于的评测用例，；

对于所有评测用例，。

解法

对于区间[l,r]
if l!=r:
	if num[l]>num[r]:
		可以翻转
elif [l+1,r-1]in [l,r] and [_l,_r]可以翻转:
	可以翻转

动态规划，根据对称性，优化成一维数组

#include <bits/stdc++.h>
using namespace std;
#define N 5005
char num[N];
int n;
long long res;
bool f[N * 2];
signed main()
{
    scanf("%s", num);
    n = strlen(num);
    for (register int k = 1; k < n; k++)
    {
        for (register int i = n - k - 1; i >= 0; i--)//正着也一样
        {
            int j = i + k;
            if (num[i] > num[j])//可以翻转
            {
                res++;
                f[i + j] = true;
            }
            else if (num[i] == num[j])//看区间[i+1,j-1]是否可以翻转
            {
                if (f[i + j])
                    res++;
            }
            else//不可以翻转
            {
                f[i+j]=false;
            }
        }
    }
    printf("%lld\n", res);
    return 0;
}

[蓝桥杯 2023 省 A] 颜色平衡树

题目描述

给定一棵树，结点由至编号，其中结点是树根。树的每个点有一个颜色。

如果一棵树中存在的每种颜色的结点个数都相同，则我们称它是一棵颜色平衡树。

求出这棵树中有多少个子树是颜色平衡树。

输入格式

输入的第一行包含一个整数，表示树的结点数。

接下来行，每行包含两个整数，用一个空格分隔，表示第个结点的颜色和父亲结点编号。

特别地，输入数据保证为，也即号点没有父亲结点。保证输入数据是一棵树。

输出格式

输出一行包含一个整数表示答案。

样例 #1

样例输入 #1

样例输出 #1

提示

【样例说明】

编号为的个结点对应的子树为颜色平衡树。

【评测用例规模与约定】

对于的评测用例，，；

对于所有评测用例，，，。

解法

```

# [蓝桥杯 2023 省 A] 买瓜

## 题目描述

小蓝正在一个瓜摊上买瓜。瓜摊上共有 $n$ 个瓜，每个瓜的重量为 $A_i$。小蓝刀功了得，他可以把任何瓜劈成完全等重的两份，不过每个瓜只能劈一刀。

小蓝希望买到的瓜的重量的和恰好为 $m$。

请问小蓝至少要劈多少个瓜才能买到重量恰好为 $m$ 的瓜。如果无论怎样小蓝都无法得到总重恰好为 $m$ 的瓜，请输出 $-1$。

## 输入格式

输入的第一行包含两个整数 $n,m$，用一个空格分隔，分别表示瓜的个数和小蓝想买到的瓜的总重量。

第二行包含 $n$ 个整数 $A_i$，相邻整数之间使用一个空格分隔，分别表示每个瓜的重量。

## 输出格式

输出一行包含一个整数表示答案。

## 样例 #1

### 样例输入 #1

3 10
1 3 13

1
2
3


### 样例输出 #1


## 提示

#### 【评测用例规模与约定】

对于 $20 \%$ 的评测用例，$n \leq 10$;

对于 $60 \%$ 的评测用例，$n \leq 20$;

对于所有评测用例，$1 \leq n \leq 30$，$1 \leq A_i \leq 10^9$，$1 \leq m \leq 10^9$。

## 前情提要🍉(bushi)

<iframe src="https://player.bilibili.com/player.html?aid=448136466&bvid=BV14j41117D6&cid=1259813341&p=1" scrolling="no" border="0" frameborder="no" framespacing="0" allowfullscreen="true" style="position: absolute; width: 1000px; left: 0; top: 0;"> </iframe>

## 解法
（瞅了一眼标签，折半搜索？跟生瓜蛋子一样不熟）
西瓜对半切/不切，不妨乘二，当作一个西瓜/两个西瓜来做
先贪心排序，优先找大瓜。
然后深度优先搜索，根据质量上下超限（小于要求质量用后缀和判断）、劈瓜数已大于当前最小答案来剪枝。
```cpp
#include<bits/stdc++.h>
using ll=long long;
const int N=32;
using namespace std;
int n,mid,m;//西瓜总数量，一半数量，要求总质量
int ans=INT_MAX;//答案
int a[N];//有一个人前来买瓜
ll sum[N];//后缀和,用来剪枝
void dfs(int i,int num,int weight){//到哪个瓜了，劈了多少瓜，买了几斤瓜
    if(weight>=m){
        if(weight==m)
            ans=min(ans,num);
        return;
    }
    if(i==n||num>=ans||weight+sum[i]<m)//超总数的递归出口，超过最小劈瓜数递归，质量不足以达到要求数剪枝
        return;
    dfs(i+1,num,weight+(a[i]<<1));//卖你生瓜蛋子
    dfs(i+1,num+1,weight+a[i]);//你**劈我瓜是吧！
    dfs(i+1,num,weight);//你要不要吧
}
int main() {
    scanf("%d%d",&n,&m);
    mid=n/2;
    m*=2;
    for(int i=0;i<n;i++){
        scanf("%d",&a[i]);
    }
    sort(a,a+n,greater<>());//从大到小贪心
    for(int i=n-1;i>=0;i--){
        sum[i]=sum[i+1]+(a[i]<<1);//求后缀和
    }
    dfs(0,0,0);
    if(ans==INT_MAX)
        ans=-1;
    printf("%d\n",ans);
    return 0;
}

[蓝桥杯 2023 省 A] 网络稳定性

题目描述

有一个局域网，由个设备和条物理连接组成，第条连接的稳定性为。

对于从设备到设备的一条经过了若干个物理连接的路径，我们记这条路径的稳定性为其经过所有连接中稳定性最低的那个。

我们记设备到设备之间通信的稳定性为至的所有可行路径的稳定性中最高的那一条。

给定局域网中的设备的物理连接情况，求出若干组设备和之间的通信稳定性。如果两台设备之间不存在任何路径，请输出。

输入格式

输入的第一行包含三个整数，分别表示设备数、物理连接数和询问数。

接下来行，每行包含三个整数，分别表示和之间有一条稳定性为的物理连接。

接下来行，每行包含两个整数，表示查询和之间的通信稳定性。

输出格式

输出行，每行包含一个整数依次表示每个询问的答案。

样例 #1

样例输入 #1

样例输出 #1

1
2
3

-1
3
5

提示

【评测用例规模与约定】

对于的评测用例，，；

对于所有评测用例，，，，，，。

解法

```

---

# [蓝桥杯 2023 省 A] 异或和之和

## 题目描述

给定一个数组 $A_i$，分别求其每个子段的异或和，并求出它们的和。或者说，对于每组满足 $1 \leq L \leq R \leq n$ 的 $L,R$，求出数组中第 $L$ 至第 $R$ 个元素的异或和。然后输出每组 $L,R$ 得到的结果加起来的值。

## 输入格式

输入的第一行包含一个整数 $n$ 。

第二行包含 $n$ 个整数 $A_i$，相邻整数之间使用一个空格分隔。

## 输出格式

输出一行包含一个整数表示答案。

## 样例 #1

### 样例输入 #1

5
1 2 3 4 5

1
2
3


### 样例输出 #1

39
```

提示

【评测用例规模与约定】

对于的评测用例，；

对于的评测用例，;

对于所有评测用例，，。

解法

异或的性质

$异或和异或和$
（没什么，复习一下）

设序列为，从到的异或和为，从到的异或前缀和为,则

即对~个前缀和，两两异或的和。
按二进制位数相加
```cpp

include

using namespace std;
using ll=long long;
const int N=(1e5)+5;
int n;
int f[N];
ll res=0ll;
int main() {
int a;
scanf(“%d”,&n);
for(int i=1;i<=n;i++){
scanf(“%d”,&a);
f[i]=f[i-1]^a;
}
int bei=1;//位权
for(int i=0;i<=20;i++){//20位二进制
int numof1=0,numof0=1;
ll sum=0;
for(int j=1;j<=n;j++){
if(f[j]&1){//最低一位1^0=1
sum+=numof0;
numof1++;
}else{//最低一位0^1=1
sum+=numof1;
numof0++;
}
f[j]>>=1;//下一位
}
res+=sum*bei;
bei<<=1;//位权翻倍
}
cout<<res<<endl;
return 0;
}
```..