2021年蓝桥杯省赛C/C++大学A1组代码

发表于 分类于 阅读次数： 本文字数： 3.9k 阅读时长 ≈ 14 分钟

算了，寒假里做几道放几道呗

P8740 [蓝桥杯 2021 省 A] 填空问题

题目描述

试题 A：卡片

【问题描述】

小蓝有很多数字卡片，每张卡片上都是数字 到 。

小蓝准备用这些卡片来拼一些数，他想从 开始拼出正整数，每拼一个，就保存起来，卡片就不能用来拼其它数了。

小蓝想知道自己能从 拼到多少。

例如，当小蓝有 张卡片，其中 到 各 张，则小蓝可以拼出 到 ，但是拼 时卡片 已经只有一张了，不够拼出 。

现在小蓝手里有 到 的卡片各 张，共 张，请问小蓝可以从 拼到多少?

提示：建议使用计算机编程解决问题。

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

试题 B：直线

【问题描述】

在平面直角坐标系中，两点可以确定一条直线。如果有多点在一条直线上，那么这些点中任意两点确定的直线是同一条。

给定平面上 个整点 ，即横坐标是 到 (包含 和 ) 之间的整数、纵坐标是 到 (包含 和 ) 之间的整数的点。这些点一共确定了 条不同的直线。

给定平面上 个整点 ，即横坐标是 到 (包含 和 ) 之间的整数、纵坐标是 到 (包含 和 ) 之间的整数的点。请问这些点一共确定了多少条不同的直线。

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

试题 C ：货物摆放

【问题描述】

小蓝有一个超大的仓库，可以摆放很多货物。

现在，小蓝有 箱货物要摆放在仓库，每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向，每箱货物的边都必须严格平行于长、 宽、高。

小蓝希望所有的货物最终摆成一个大的立方体。即在长、宽、高的方向上分别堆 、、 的货物，满足 。

给定 ，请问有多少种堆放货物的方案满足要求。

例如，当 时，有以下 种方案：、、、 、 、

请问，当 (注意有 位数字) 时，总共有多少种方案?

提示：建议使用计算机编程解决问题。

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

试题 D：路径

【问题描述】

小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图中的最短路径。

小蓝的图由 个结点组成，依次编号 至 。

对于两个不同的结点 ，如果 和 的差的绝对值大于 ，则两个结点之间没有边相连; 如果 和 的差的绝对值小于等于 ，则两个点之间有一条长度为 和 的最小公倍数的无向边相连。

例如：结点 和结点 之间没有边相连; 结点 和结点 之间有一条无向边，长度为 ; 结点 和结点 之间有一条无向边，长度为 。

请计算，结点 和结点 之间的最短路径长度是多少。

提示：建议使用计算机编程解决问题。

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

试题 E：回路计数

【问题描述】

蓝桥学院由 栋教学楼组成，教学楼编号 到 。对于两栋教学楼 和 ，当 和 互质时， 和 之间有一条走廊直接相连，两个方向皆可通行，否则没有直接连接的走廊。

小蓝现在在第一栋教学楼，他想要访问每栋教学楼正好一次，最终回到第一栋教学楼（即走一条哈密尔顿回路)，请问他有多少种不同的访问方案? 两个访问方案不同是指存在某个 ，小蓝在两个访问方法中访问完教学楼 后访问了不同的教学楼。

提示：建议使用计算机编程解决问题。

解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
using ll = long long;
using ull = unsigned long long;
//==================== 1 ====================
void solve1()
{
    int a[10];
    for (int i = 0; i <= 9; i++)
        a[i] = 2021;
    for (int i = 1;; i++)
    {
        for (int j = i; j; j /= 10)
        {
            if (a[j % 10] == 0)
            {
                cout << i - 1 << endl;
                return;
            }
            --a[j % 10];
        }
    }
}
//==================== 2 ====================
int gcd(int x, int y)
{
    return x % y == 0 ? y : gcd(y, x % y);
}
void solve2()
{
    int n = 20, m = 21;
    ull ans = 0ll; // row,col
    for (int a = 1; a < n; a++)
    {
        for (int b = 1; b < m; b++)
        {
            if (gcd(a, b) != 1)
                continue;
            ans += (n - a) * (m - b);
            if (a * 2 <= n && b * 2 <= n)
            {
                ans -= (n - 2 * a) * (m - 2 * b);
            }
        }
    }
    ans *= 2;
    ans += (n + m);
    cout << ans << endl;
}
//==================== 3 ====================
typedef pair<ull, ull> pp;
ull ans3 = 0;
map<pp, bool> mp;
vector<ull> yz; // 因子
void dfs3(pp p, int d)
{
    if (d == yz.size())
    {
        if (!mp[p])
        {
            mp[p] = true;
            ans3++;
        }
        return;
    }
    dfs3(pp(p.first, p.second), d + 1);
    dfs3(pp(p.first * yz[d], p.second), d + 1);
    dfs3(pp(p.first, p.second * yz[d]), d + 1);
}
void solve3()
{
    ull n = 2021041820210418;
    for (int i = 2; i <= n;)
    {
        if (n % i == 0)
        {
            // cout<<i<<',';
            yz.push_back(i);
            n /= i;
        }
        else
        {
            i++;
        }
    }
    // 2,3,3,3,17,131,2857,5882353
    dfs3(pp(1, 1), 0);
    cout << ans3 << endl;
}
//==================== 4 ====================
typedef pair<int, int> pint;
void solve4()
{
    int n = 2021;
    vector<vector<pint>> g(2022);
    for (int i = 1; i <= n; i++)
    {
        for (int j = i + 1; j <= i + 21 && j <= n; j++)
        {
            int w = i * j / gcd(i, j);
            g[i].push_back(pint(w, j));
            g[j].push_back(pint(w, i));
        }
    }
    // dijsktra
    const int inf = INT_MAX;
    vector<int> dis(n + 1, inf);
    vector<bool> vis(n + 1, false);
    dis[1] = 0;
    priority_queue<pint, vector<pint>, greater<>> pq;
    pq.push(pint(0, 1));
    while (!pq.empty())
    {
        int u = pq.top().second;
        pq.pop();
        if (!vis[u])
        {
            vis[u] = true;
            for (auto [w, v] : g[u])
            {
                if (dis[v] > dis[u] + w)
                {
                    dis[v] = dis[u] + w;
                    if (!vis[v])
                        pq.push(pint(dis[v], v));
                }
            }
        }
    }
    cout << dis[2021] << endl;
}
//==================== 5 ====================
ull ans5;
int ok;
bool have[22][22];
ull f[1 << 21][22]; // 走的序列,到下一个点
void solve5()
{
    for (int i = 1; i < 21; i++)
    {
        for (int j = i + 1; j <= 21; j++)
        {
            if (gcd(i, j) == 1)
            {
                have[i][j] = have[j][i] = true;
            }
        }
    }
    ok =(1 << 21)-1;// 2,097,151
    f[1][1]=1;
    for (int c = 1; c <= ok; c++)
    {
        for (int i = 1; i <= 21; i++)
        {
            if (c & (1 << (i - 1)))
                for (int j = 1; j <= 21; j++)
                {
                    if (!(c & (1 << (j - 1))) && have[i][j])
                        f[c | (1 << (j - 1))][j] += f[c][i];
                }
        }
    }
    for (int i = 1; i <= 21; i++)
    {
        ans5 += f[ok][i];
    }
    cout << ans5 << endl;
}
//==================== answer ====================
signed main()
{
    string ans[] = {
        "3181",                 // 双引号中替换为 A 题的答案
        "40257",                // 双引号中替换为 B 题的答案
        "2430",                 // 双引号中替换为 C 题的答案
        "10266837",             // 双引号中替换为 D 题的答案
        "881012367360", // 双引号中替换为 E 题的答案
    };
    char T;
    cin >> T;
    cout << ans[T - 'A'] << endl;
    return 0;
}

P8742 [蓝桥杯 2021 省 AB] 砝码称重

题目描述

你有一架天平和 个砝码, 这 个砝码重量依次是 。 请你计算一共可以称出多少种不同的重量?

注意砝码可以放在天平两边。

输入格式

输入的第一行包含一个整数 。

第二行包含 个整数: 。

输出格式

输出一个整数代表答案。

输入输出样例 #1

输入 #1

1
2
3
1 4 6

输出 #1

1
10

说明/提示

【样例说明】

能称出的 10 种重量是: 、、、、、、、、、 。

【评测用例规模与约定】

对于 的评测用例, 。

对于所有评测用例, 个砝码总重不超过 。

蓝桥杯 2021 第一轮省赛 A 组 F 题（B 组 G 题）。

解法

01背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int f[101][N];
signed main()
{
    int n, w, sum = 0;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &w);
        sum += w;
        for (int j = sum; j; j--)
            if (f[i - 1][j])
                f[i][j] = f[i][abs(j - w)] = f[i][j + w] = 1;
        f[i][w] = 1;
    }
    int ans = 0;
    for (int j = 1; j <= sum; j++)
        ans += f[n][j];
    printf("%d\n", ans);
    return 0;
}

P8743 [蓝桥杯 2021 省 A] 异或数列

题目描述

Alice 和 Bob 正在玩一个异或数列的游戏。初始时，Alice 和 Bob 分别有一个整数 和 , 有一个给定的长度为 的公共数列 。

Alice 和 Bob 轮流操作，Alice 先手，每步可以在以下两种选项中选一种:

选项 1: 从数列中选一个 给 Alice 的数异或上, 或者说令 变为 。（其中 表示按位异或）

选项 2: 从数列中选一个 给 Bob 的数异或上，或者说令 变为 。

每个数 都只能用一次, 当所有 均被使用后（ 轮后）游戏结束。游戏结束时, 拥有的数比较大的一方获胜，如果双方数值相同，即为平手。

现在双方都足够聪明，都采用最优策略，请问谁能获胜?

输入格式

每个评测用例包含多组询问。询问之间彼此独立。

输入的第一行包含一个整数 ，表示询问数。

接下来 行每行包含一组询问。其中第 行的第一个整数 表示数列长度，随后 个整数 表示数列中的每个数。

输出格式

输出 行，依次对应每组询问的答案。

每行包含一个整数 、 或 分别表示 Alice 胜、平局或败。

输入输出样例 #1

输入 #1

1
2
3
4
5
4
1 1
1 0
2 2 1
7 992438 1006399 781139 985280 4729 872779 563580

输出 #1

1
2
3
4
1
0
1
1

说明/提示

对于所有评测用例, 。

蓝桥杯 2021 第一轮省赛 A 组 G 题。

解法

转换成二进制，对于某一位，如果它是1，则反转这一位答案。0对答案无影响。奇数个1异或得1，偶数个1异或得0

  • 当1有偶数个时，偶数=偶数+偶数，这一位平手。
  • 当1有奇数个时，奇数=奇数+偶数，两人都想办法获得奇数个1。
    • 只有一个1，Alice直接选，Alice win
    • 当0有偶数个，两人相抵，Alice win
    • 当0有奇数个，Bob选一个0，反转局面，Bob win

例:1 1 1 0 0 0
Alice:1
Bob:0(反转先手)
Alice:0
Bob:0
Alice:1(被迫)
Bob:Alice 1
Bob win

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>
using namespace std;
signed main()
{
    int t, n, x, cnt[22];
    scanf("%d", &t);
    while (t--)
    {
        scanf("%d", &n);
        memset(cnt, 0, sizeof(cnt));
        for (int i = 0; i < n; i++)
        {
            scanf("%d", &x);
            for (int b = 0; x; b++)
            {
                if (x & 1)
                    cnt[b]++;
                x >>= 1;
            }
        }
        int win = 0;
        for (int i = 20; i >= 0; i--)
        {
            if (cnt[i] & 1)
            {
                if (cnt[i] == 1)
                    win = 1;
                else
                    win = n & 1 ? 1 : -1; // 偶数个0Alice win
                break;
            }
        }
        printf("%d\n", win);
    }
    return 0;
}
/*

*/

P8744 [蓝桥杯 2021 省 A] 左孩子右兄弟

题目描述

对于一棵多叉树，我们可以通过“左孩子右兄弟”表示法，将其转化成一棵二叉树。

如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。

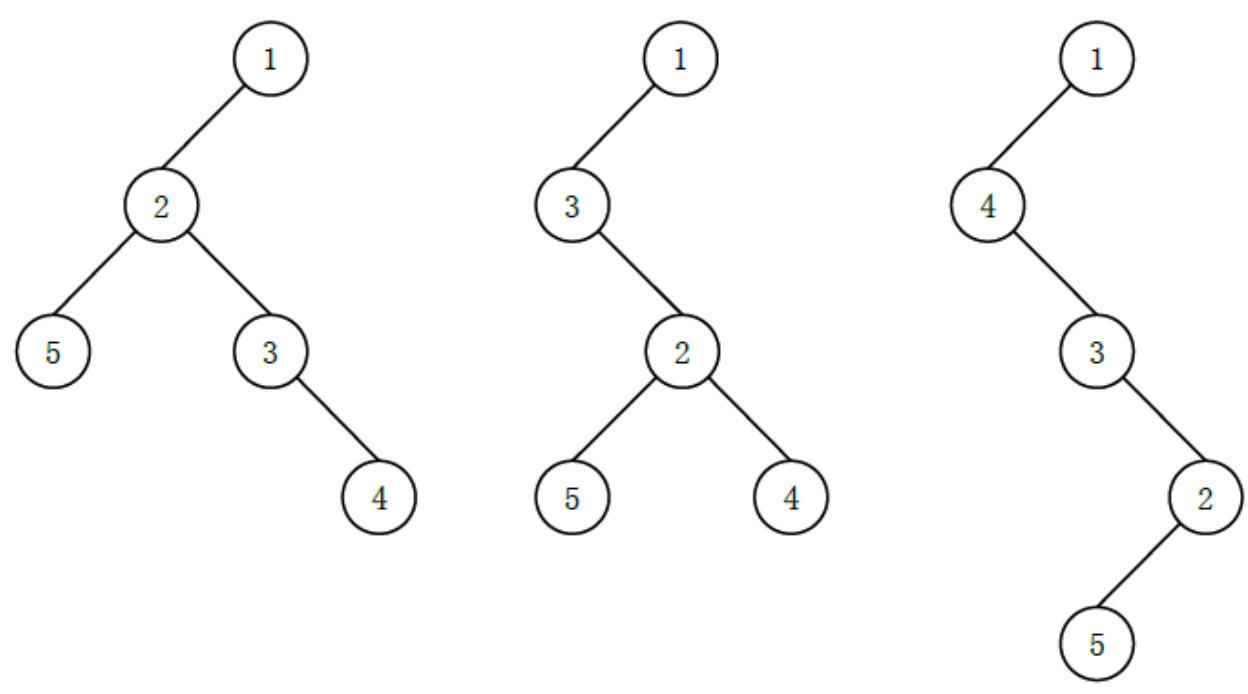
给定一棵包含 个结点的多叉树，结点从 至 编号，其中 号结点是根，每个结点的父结点的编号比自己的编号小。请你计算其通过”左孩子右兄弟”表示法转化成的二叉树，高度最高是多少。（只有根结点这一个结点的树高度为 ）

例如如下的多叉树：

可能有以下 种 (这里只列出 种, 并不是全部) 不同的 “左孩子右兄弟” 表示:

其中最后一种高度最高, 为 。

输入格式

输入的第一行包含一个整数 。

以下 行, 每行包含一个整数, 依次表示 至 号结点的父结点编号。

输出格式

输出一个整数表示答案。

输入输出样例 #1

输入 #1

1
2
3
4
5
5
1
1
1
2

输出 #1

1
4

说明/提示

对于 的评测用例，;

对于所有评测用例， 。

蓝桥杯 2021 第一轮省赛 A 组 H 题。

解法

dfs
最大答案=孩子数+孩子中的最大答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n;
vector<vector<int>> child(N);
int dfs(int u)
{
    int ret = 0;
    for (int v : child[u])
        ret = max(ret, dfs(v));
    return ret + child[u].size();
}
signed main()
{
    scanf("%d", &n);
    int r;
    for (int i = 2; i <= n; i++)
    {
        scanf("%d", &r);
        child[r].push_back(i);
    }
    printf("%d", dfs(1));
    return 0;
}

P8745 [蓝桥杯 2021 省 AB] 括号序列

题目描述

给定一个括号序列，要求尽可能少地添加若干括号使得括号序列变得合法，当添加完成后，会产生不同的添加结果，请问有多少种本质不同的添加结果。两个结果是本质不同的是指存在某个位置一个结果是左括号，而另一个是右括号。

例如，对于括号序列 ((()，只需要添加两个括号就能让其合法，有以下几种不同的添加结果：()()() 、()(())、(())()、(()()) 和 ((()))。

输入格式

输入一行包含一个字符串 ，表示给定的括号序列，序列中只有左括号和右括号。

输出格式

输出一个整数表示答案，答案可能很大，请输出答案除以 （即 ）的余数。

输入输出样例 #1

输入 #1

1
((()

输出 #1

1
5

说明/提示

对于 的评测用例，。

对于所有评测用例，。

蓝桥杯 2021 第一轮省赛 A 组 I 题（B 组 J 题）。

解法

python生成代码

1
2
3
4
5
6
7
8
a=['(',')']
from random import randint
def f():
    l=randint(5,12)
    for i in range(l):
        print(a[randint(0,1)],end='')
    print()
f()

嗯。。。后面没有做了（逃）