2025年蓝桥杯省赛C/C++大学A1组代码

发表于 分类于 阅读次数： 本文字数： 6k 阅读时长 ≈ 22 分钟

一雪2024的前耻，今年报销了300大洋报名费！慢慢复盘。

考时黑客不会优化，最后一题只写完了拖布，拓步，托……反正就是那个什么什么排序啦！目前黑客已经优化，最后三题还没复盘。

洛谷评测

注意事项

  • 这里的题解偷懒了，实际上考试时不要用ios::sync_with_stdio(false);cin.tie(nullptr), cout.tie(nullptr);，直接用scanf和printf最保险
  • 注意数据范围，注意用long long或者unsigned long long的情况
  • 一定记得return 0
  • 注意devcpp开栈和c++版本
  • 某些特殊的填空题可以用python写，改天新开一篇博文写
  • 写一题交一题
  • 拿不要死磕一道题，尽可能每道题都暴力骗到分。实在不行直接输出样例。

P12138 [蓝桥杯 2025 省 A] 寻找质数

题目背景

本站蓝桥杯 2025 省赛测试数据均为洛谷自造，与官方数据可能存在差异，仅供学习参考。

题目描述

如果一个正整数只能被 和它本身两个数整除，就称为一个质数。最小的几个质数依次是

请问，第 个质数是多少？

输入格式

无

输出格式

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只需要编写一个程序输出这个整数，输出多余的内容将无法得分。

解法

get 5/5分
暴力就好

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int cnt = 1, n = 1;
while (cnt < 2025)
{
    n += 2;
    bool prime = true;
    for (int i = 3; i < n; i += 2)
    {
        if (n % i == 0)
        {
            prime = false;
            break;
        }
    }
    if (prime)
    {
        ++cnt;
    }
}
cout << n << endl;

P12139 [蓝桥杯 2025 省 A] 黑白棋

题目描述

小蓝最近迷上了一款名为“黑白棋填充”的游戏。该游戏在一个方形网格棋盘上进行，其中部分格子已经填有黑色或白色的棋子，而其他格子为空，等待玩家填入棋子。

游戏规则是，玩家需要按照以下规则填满整个棋盘，才能算作胜利：

  1. 黑白棋子数量均等：
    在每一行和每一列中，黑色棋子和白色棋子的数量必须相等。
  2. 相邻棋子限制：
    在棋盘的任何一行或一列中，不能有超过两个相同颜色的棋子连续排列（即不允许出现“黑黑黑”或“白白白”的情况）。
  3. 行列唯一性：
    每一行的棋子排列方式必须是唯一的，不能与棋盘中的任何其他行完全相同。
    每一列的棋子排列方式必须是唯一的，不能与棋盘中的任何其他列完全相同。
    行与列之间的棋子排列不作比较，即行可以与列相同，无需满足行列间的唯一性。

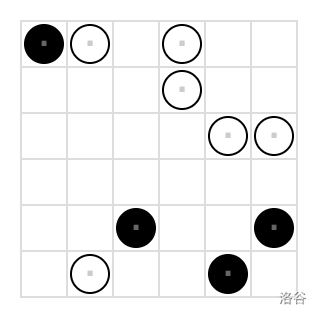
现在有一个 的棋盘，如上图所示，其中部分格子已填入棋子（黑色或白色），其余格子需要你填充，题目保证有唯一解。

请给出唯一的正确解，并按照以下格式输出答案：

  • 黑色棋子用 表示，白色棋子用 表示。
  • 从左到右、从上到下的顺序，依次遍历棋盘上的所有格子，并将这些值拼接成一个长度为 的字符串。

例如，假设最终填充完成后的棋盘如下（仅为示例，并非真实答案）：

1
2
3
4
5
6
1 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 1 0 0 0
0 0 1 1 0 0
0 0 1 1 1 1

则输出结果应为：100000000000000000001000001100001111。

输入格式

无

输出格式

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只需要编写一个程序输出这个整数，输出多余的内容将无法得分。

解法

get 5/5分
考试时第一反应是打excel表格，好吧。其实dfs稍微剪枝一下就可以。狠狠暴力！忘情地暴力！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
#include <bits/stdc++.h>

using namespace std;
using ll = long long;
int board[][6] = {
    {1, 0, 2, 0, 2, 2},
    {2, 2, 2, 0, 2, 2},
    {2, 2, 2, 2, 0, 0},
    {2, 2, 2, 2, 2, 2},
    {2, 2, 1, 2, 2, 1},
    {2, 0, 2, 2, 1, 2}};
// 颜色，对应剩余棋子数
int row[2][6] = {{3, 3, 3, 3, 3, 3}, {3, 3, 3, 3, 3, 3}},
    col[2][6] = {{3, 3, 3, 3, 3, 3}, {3, 3, 3, 3, 3, 3}};
void dfs(int r, int c)
{
    if (r == 5) // 列尾
    {
        //每一列的棋子排列方式必须是唯一的，不能与棋盘中的任何其他列完全相同。
        for (int j = 0; j < c - 1; ++j)
        {
            bool ok = false;
            for (int i = 0; i < 6; ++i)
            {
                if (board[i][j] != board[i][c - 1])
                {
                    ok = true;
                    break;
                }
            }
            if (!ok)
                return;
        }
    }
    if (c == 6) // 行尾
    {
        // 每一行的棋子排列方式必须是唯一的，不能与棋盘中的任何其他行完全相同。
        for (int i = 0; i < r; ++i)
        {
            bool ok = false;
            for (int j = 0; j < 6; ++j)
            {
                if (board[i][j] != board[r][j])
                {
                    ok = true;
                    break;
                }
            }
            if (!ok)
                return;
        }
        ++r;
        c = 0;
    }
    if (r == 6) // 列尾
    {
        for (int i = 0; i < 6; ++i)
        {
            for (int j = 0; j < 6; ++j)
            {
                cout << board[i][j];
            }
            // cout << endl;
        }
        exit(0);
    }
    // 该位置为空
    if (board[r][c] == 2)
    {
        for (int color = 0; color < 2; color++)
        {
            // 每一行和每一列中，黑色棋子和白色棋子的数量必须相等
            if (row[color][r] <= 0 || col[color][c] <= 0)
                continue;
            // 在棋盘的任何一行或一列中，不能有超过两个相同颜色的棋子连续排列（即不允许出现“黑黑黑”或“白白白”的情况）。
            if (r >= 2 && color == board[r - 1][c] && color == board[r - 2][c])
                continue;
            if (c >= 2 && color == board[r][c - 1] && color == board[r][c - 2])
                continue;
            --row[color][r];
            --col[color][c];
            board[r][c] = color;
            dfs(r, c + 1);
            ++row[color][r];
            ++col[color][c];
        }
        board[r][c] = 2;
    }
    else // 该位置已经有棋子
    {
        int color = board[r][c];
        // 每一行和每一列中，黑色棋子和白色棋子的数量必须相等
        if (row[color][r] <= 0 || col[color][c] <= 0)
            return;
        // 在棋盘的任何一行或一列中，不能有超过两个相同颜色的棋子连续排列（即不允许出现“黑黑黑”或“白白白”的情况）。
        if (r >= 2 && color == board[r - 1][c] && color == board[r - 2][c])
            return;
        if (c >= 2 && color == board[r][c - 1] && color == board[r][c - 2])
            return;
        --row[color][r];
        --col[color][c];
        dfs(r, c + 1);
        ++row[color][r];
        ++col[color][c];
    }
}
signed main()
{
    dfs(0, 0);//101001010011101100010110011001100110
    return 0;
}

P12140 [蓝桥杯 2025 省 A] 抽奖

题目背景

本站蓝桥杯 2025 省赛测试数据均为洛谷自造，与官方数据可能存在差异，仅供学习参考。

题目描述

LQ 商场为了回馈广大用户，为在此消费的用户提供了抽奖机会：抽奖机有三个转轮，每个转轮上都分布有 个数字图案，标号为 ，按照从 到 顺序转动，当转到第 个图案时会从第一个继续开始。奖项如下：

  1. 三个相同的图案，积分 ；
  2. 两个相同的图案，积分 ；
  3. 三个数字图案，从左到右连续（例如 ），积分 ；
  4. 三个数字图案，经过顺序调整后连续（例如 或 ），积分 ；

抽奖机处于初始状态，三个转轮都处于第一个位置。每次开始抽奖，都会产生三个对应的随机数 ，表示第 个转轮会向后转动 次停下。下次抽奖时，转轮会从上一次转动后的位置开始继续转动。

注意，一次抽奖最多只能获得一次积分，如果同时命中多个奖项，以积分最大的那个奖项为准。

请问，如果执行 次抽奖，总积分值是多少？

输入格式

输入的第一行包含一个正整数 ，表示转轮大小。

第二行包含 个正整数 ，依次表示第一个转轮上的数字图案，相邻整数之间使用一个空格分隔。

第三行包含 个正整数 ，依次表示第二个转轮上的数字图案，相邻整数之间使用一个空格分隔。

第四行包含 个正整数 ，依次表示第三个转轮上的数字图案，相邻整数之间使用一个空格分隔。

第五行包含一个整数 ，表示抽奖次数。

接下来 行，每行包含三个正整数 ，相邻整数之间使用一个空格分隔。

输出格式

输出一行包含一个整数表示答案，即 次抽奖累计获得的积分的值。

输入输出样例 #1

输入 #1

1
2
3
4
5
6
7
8
4
3 2 4 1
2 2 2 2
4 3 0 9
3
4 4 4
3 1 1
40 39 2

输出 #1

1
300

说明/提示

样例说明

  • 第一次抽奖：三个转轮都转动 次，到达位置 ，数字图案为 ，积分 ；
  • 第二次抽奖：数字图案为 ，积分 ；
  • 第三次抽奖：数字图案为 ，积分不增加。

评测用例规模与约定

  • 对于 的评测用例，，；
  • 对于 的评测用例，，；
  • 对于 的评测用例，，；
  • 对于 的评测用例，，；
  • 对于所有评测用例，，，，。

解法

大模拟，暴力。注意转盘用%运算模拟

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>
using namespace std;
#define N 1005

int n, m, d, res = 0;
int arr[3][N];
int pos[3], jiang[3];
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);

    cin >> n;
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < n; ++j)
            cin >> arr[i][j];
    cin >> m;
    while (m--)
    {
        for (int i = 0; i < 3; ++i)
        {
            cin >> d;
            pos[i] = (pos[i] + d) % n;
            jiang[i] = arr[i][pos[i]];
        }
        if (jiang[0] == jiang[1])
        {
            if (jiang[0] == jiang[2])
                res += 200;
            else
                res += 100;
        }
        else if (jiang[0] == jiang[2] || jiang[1] == jiang[2])
        {
            res += 100;
        }
        else if (jiang[0] + 1 == jiang[1] && jiang[0] + 2 == jiang[2])
        {
            res += 200;
        }
        else
        {
            sort(jiang, jiang + 3);
            if (jiang[0] + 1 == jiang[1] && jiang[0] + 2 == jiang[2])
            {
                res += 100;
            }
        }
    }
    cout << res << endl;
    return 0;
}

P12141 [蓝桥杯 2025 省 A] 红黑树

题目描述

小蓝最近学习了红黑树，红黑树是一种特殊的二叉树，树上的结点有两种类型：红色结点和黑色结点。

小蓝在脑海中构造出一棵红黑树，构造方式如下：

  1. 根结点是一个红色结点；
  2. 如果当前结点 是红色结点，那么左子结点 是红色结点，右子结点 是黑色结点；
  3. 如果当前结点 是黑色结点，那么左子结点 是黑色结点，右子结点 是红色结点；

此二叉树前几层的形态如下图所示：

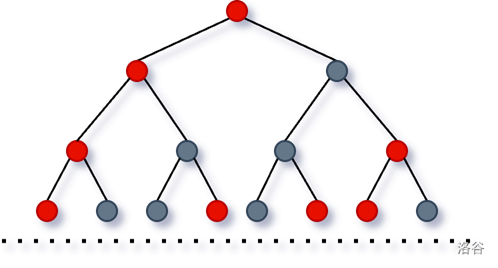
小蓝会从树上随机挑选结点，请你帮忙判断他选出的是红色结点还是黑色结点。

输入格式

输入的第一行包含一个正整数 ，表示小蓝挑选的结点数。

接下来 行，每行包含两个正整数 ，用一个空格分隔，表示小蓝挑选的结点是第 行（从上往下数）第 个（从左往右数）结点。

输出格式

输出 行，每行包含一个字符串，依次表示小蓝每次挑选的结点的答案。RED 表示红色结点，BLACK 表示黑色结点。

输入输出样例 #1

输入 #1

1
2
3
2
1 1
2 2

输出 #1

1
2
RED
BLACK

说明/提示

样例说明

  • 第一行第一个结点为根结点，红色；
  • 第二行第二个结点为黑色结点。

评测用例规模与约定

  • 对于 的评测用例，，；
  • 对于 的评测用例，，；
  • 对于 的评测用例，，；
  • 对于 的评测用例，，；
  • 对于所有评测用例，，，。

解法

get 10/10
使用瞪眼法，一眼顶针，红黑树看出是异或运算，多往下画两行就发现，颜色和行数无关。把红和黑分别看作0和1，颜色就是异或1的运算。
红黑树示意图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int n, m, k;
cin >> m;
while (m--)
{
    cin >> n >> k;
    int a = 0;
    --k;
    while (k)
    {
        a ^= (k & 1);
        k >>= 1;
    }
    if (a)
        cout << "BLACK" << endl;
    else
        cout << "RED" << endl;
}

P12142 [蓝桥杯 2025 省 A] 黑客

题目描述

小蓝正在两台电脑之间拷贝数据，数据是一个 大小的正整数矩阵，因此总共有 个由空格分开的整数，其中前两个整数分别为 和 。然而，有黑客入侵了小蓝的电脑，导致这 个正整数的顺序被打乱了。小蓝想知道最多可能有多少个不同的原矩阵。

两个矩阵相同当且仅当它们行数相同、列数相同，且每个位置上的数相同。

输入格式

输入的第一行包含一个正整数 。

第二行包含 个正整数 ，相邻整数之间使用一个空格分隔。

输出格式

输出一行包含一个整数表示答案。答案可能很大，请输出答案除以 的余数。

输入输出样例 #1

输入 #1

1
2
6
2 2 1 4 3 3

输出 #1

1
24

说明/提示

样例说明

可能的原矩阵情况包括：

  1. ：有 种原矩阵：；
  2. ：有 种原矩阵；
  3. ：有 种原矩阵；

总计 种。

评测用例规模与约定

  • 对于 的评测用例，；
  • 对于所有评测用例，，。

解法

思路

不用管是不是二维矩阵，直接看作一维数矩阵。题目大意：当找到两个数 和 ，当 时，求剩余 个数有多少种不重复的排列，并对其求和。

考试时不知道带模的除法怎么做，只好开了 unsigned long long 并且打了个 22 以内的阶乘表，大概是拿 40% 的分了。

实际上，后面补习数论，模意义下的除法是这样的：

其中 是求 的模意义下的逆元。这里数据量不大，可以套快速幂公式。

而这里的排列公式为：当有 个不相同的数 排列，对于每一个数 ，它的数量是 ，排列方式有 种。

豪！基础复习完毕。回到题目——

对于行数 和列数 ，当 时，求剩余 个数的排列方式数目。排列公式分母里要去掉一个 和一个 ，当两者相同时，就相当于去掉两个 。

对于一对“行数”和“列数”，上述排列公式的分母如下：

将分母带入排列公式：

最终答案表达式，即求和：

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
using namespace std;
#define ll unsigned long long
#define N 500005
const int p = 1000000007;

int n, m;
unordered_map<ll, int> mp;//对每个数，对应的数量。unordered_map比map更高效
ll jc[N]; // 阶乘
ll inverse(ll a)//快速幂逆元
{
    ll b = p - 2, ret = 1;
    while (b)
    {
        if (b & 1)
            ret = ret * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ret;
}
signed main()
{
    jc[0] = jc[1] = 1;
    for (int i = 2; i < N; ++i)
    {
        jc[i] = jc[i - 1] * i % p;
    }
    scanf("%d", &n);
    m = n - 2;//矩阵的大小
    ll a, b = 1, rc = 0;
    for (int i = 0; i < n; ++i)
    {
        scanf("%lld", &a);
        ++mp[a];
    }
    for (auto i : mp)
    {
        b = b * jc[i.second] % p;
    }
    for (auto r : mp)
    {
        if (m % r.first != 0)
            continue;
        auto c = mp.find(m / r.first);
        if (c == mp.end()) // 找不到两数相乘为n-2
            continue;
        if (r.first != c->first)
            rc = (rc + r.second * c->second % p) % p;
        else
            rc = (rc + r.second * (r.second - 1) % p) % p;
    }
    cout << jc[n - 2] * inverse(b) % p * rc % p << endl;
    return 0;
}

P12143 [蓝桥杯 2025 省 A] 好串的数目

题目描述

对于一个长度为 的字符串 来说，子串的定义是从中选出两个下标 ，这之间所有的字符组合起来的一个新的字符串： 就是其中一个子串。

现在给出一个只有数字字符 组成的数字字符串，小蓝想要知道在其所有的子串中，有多少个子串是好串。一个子串是好串，当且仅当它满足以下两个条件之一：

  1. 单字符子串一定是好串，即当子串长度为 时，它总是好串；
  2. 长度大于 时，可以拆分为两个连续非递减子串：
    一个串 为连续非递减子串是指，对于所有 ，满足 或 。即数字串中的每一个数字，要么等于上一个数字，要么等于上一个数字加 。例如 12233、456 是连续非递减子串。

输入格式

输入一行包含一个字符串 。

输出格式

输出一行包含一个整数表示答案，即好串的数目。

输入输出样例 #1

输入 #1

1
12258

输出 #1

1
12

输入输出样例 #2

输入 #2

1
97856

输出 #2

1
13

说明/提示

样例说明 1

  • 长度为 的好串：1、2、2、5、8，共 个；
  • 长度为 的好串：12、22、25、58，共 个；
  • 长度为 的好串：122、225，共 个；
  • 长度为 的好串：1225，共 个；

总计 个。

样例说明 2

  • 长度为 的好串：9、7、8、5、6，共 个；
  • 长度为 的好串：97、78、85、56，共 个；
  • 长度为 的好串：978、785、856，共 个；
  • 长度为 的好串：7856，共 个；

总计 个。

评测用例规模与约定

  • 对于 的评测用例，；
  • 对于 的评测用例，；
  • 对于 的评测用例，；
  • 对于 的评测用例，；
  • 对于 的评测用例，；
  • 对于所有评测用例，， 中只包含数字字符 。

解法

找规律

P12144 [蓝桥杯 2025 省 A] 地雷阵

题目描述

小蓝正在平面直角坐标系中的第一象限里玩一个逃生小游戏。在第一象限中埋有 颗地雷，第 颗地雷的坐标为 ，触发范围为以 为圆心，半径为 的圆。一旦小蓝走进了圆内就会触发地雷导致游戏失败。小蓝初始在原点 上，他需要在第一象限内选择一个方向一直往前走，如果能不触发任何地雷即可成功通关游戏。他想知道在 中均匀随机选择一个方向，即在 （朝向 轴正方向）至 （朝向 轴正方向）之间随机选择一个方向，通关游戏的概率是多少？

输入格式

输入的第一行包含一个正整数 。

接下来 行，每行包含三个正整数 ，相邻整数之间使用一个空格分隔。

输出格式

输出一行包含一个实数，四舍五入保留三位小数，表示答案。

输入输出样例 #1

输入 #1

1
2
1
2 2 1

输出 #1

1
0.540

输入输出样例 #2

输入 #2

1
2
3
2
1 3 1
3 1 1

输出 #2

1
0.181

说明/提示

评测用例规模与约定

  • 对于 的评测用例，；
  • 对于所有评测用例，，，。

解法

根据圆形切线的性质，每一个圆都可以对应一个角度范围。对角度范围进行排序，就是一个线段覆盖的贪心问题。

碎碎念 注意反三角函数在C++里是atan,还有他是弧度还是角度？π 以及它的各个倍数在C++里也是有现成的值，好像是什么M_PI？我当时直接跑到文件夹里搜索的（）而且应该是有弧度角度转换的函数吧

P12145 [蓝桥杯 2025 省 A] 扫地机器人

题目描述

在一个含有 个点 条边的无重边无自环的连通无向图中，有一个扫地机器人在执行清扫作业。其中结点 的标记 ：如果为 ，则说明该结点需要进行清扫，扫地机器人在到达这个结点时会顺便进行清扫工作。机器人想知道，如果选定任意结点出发，每条边只能经过一次的话，最多能清扫多少个待清扫结点？

输入格式

输入的第一行包含一个正整数 。

第二行包含 个整数 ，相邻整数之间使用一个空格分隔。

接下来 行，每行包含两个正整数 ，用一个空格分隔，表示结点 和结点 之间有一条边。

输出格式

输出一行包含一个整数表示答案。

输入输出样例 #1

输入 #1

1
2
3
4
5
6
7
8
9
10
11
9
1 0 1 0 0 1 1 0 1
2 8
2 9
2 5
1 5
1 3
1 4
4 5
4 6
6 7

输出 #1

1
4

说明/提示

样例说明

其中一种可行路线：，清扫结点 （共 个）。

评测用例规模与约定

  • 对于 的评测用例，；
  • 对于所有评测用例，，，。

解法

一眼顶针，题目里的图为 个结点和 条边的连通图。当有 个结点和 条边的连通图，这是一颗树，树再加上一条边，就是只有一个环的图。除了一个环，剩下都是树的图，即基环树。

题意：一个基环树，每个点的权值为0或1，选择一条链，点不能走重复，权值总和最大。

那么，我们的最佳路线，有可能有三种：

  1. 从叶子结点出发，到某一个祖先，再跑到另一个叶子结点
  2. 从叶子结点出发，走到环绕到另一个分岔路口，再走到另一个叶子结点；
  3. 同样从叶子结点出发，走到环跑一圈；或者根本没有叶子结点，直接跑一圈。
    基环树
    这时候可以从叶子结点开始拓补排序，得到从这个环结点进出环的点权值之和。
    考试的时候就只写完了拓补排序，还没有跑环就到时间了。最后一题也算了。